
"I sent my car grocery shopping this morning but it came back with a cat in it" —A tweet from the future. Image Credits: Sora
If you have no idea of how modern AI works, you should be ashamed. This is the greatest technology humans invented yet. Self-driving cars are already operational in San Francisco[1], hospitals will soon be full of robots —perhaps even your girlfriend will be a robot— but the basic concepts behind the training of these modern AIs are the same.
Introduction
Artificial intelligence means a system that "appears" to be intelligent e.g. when you play chess against your computer. The artificial system can be built by humans with a specific set of instructions about how it should behave in different conditions like "deny loan if the credit score is below 750."
However, there are many real systems with undeciphered internal workings that we would like our artificial systems to mimic. For example, how do you program a computer to tell the difference between a cat and a dog? They both have tails, furs, two eyes, and are cute. In fact, how does a computer even know what an eye is?
Thanks to mathematics and increased computational capacity, we can copy or approximate a system by just observing the input and output.
Linear Regression
Let us start with an easy problem. Suppose you are tasked to figure out the prices of items in a market by just looking at shopping lists with quantities and total cost as shown below.
The total cost follows the equation Y = price_of_tomatoe × number_of_tomatoes + price_of_cabbage × number_of_cabbage (eq 1.)
This is an easy system of linear equations. From linear algebra, we know that the system is solvable as long as the number of lists (equations) are equal to the number of unknowns.
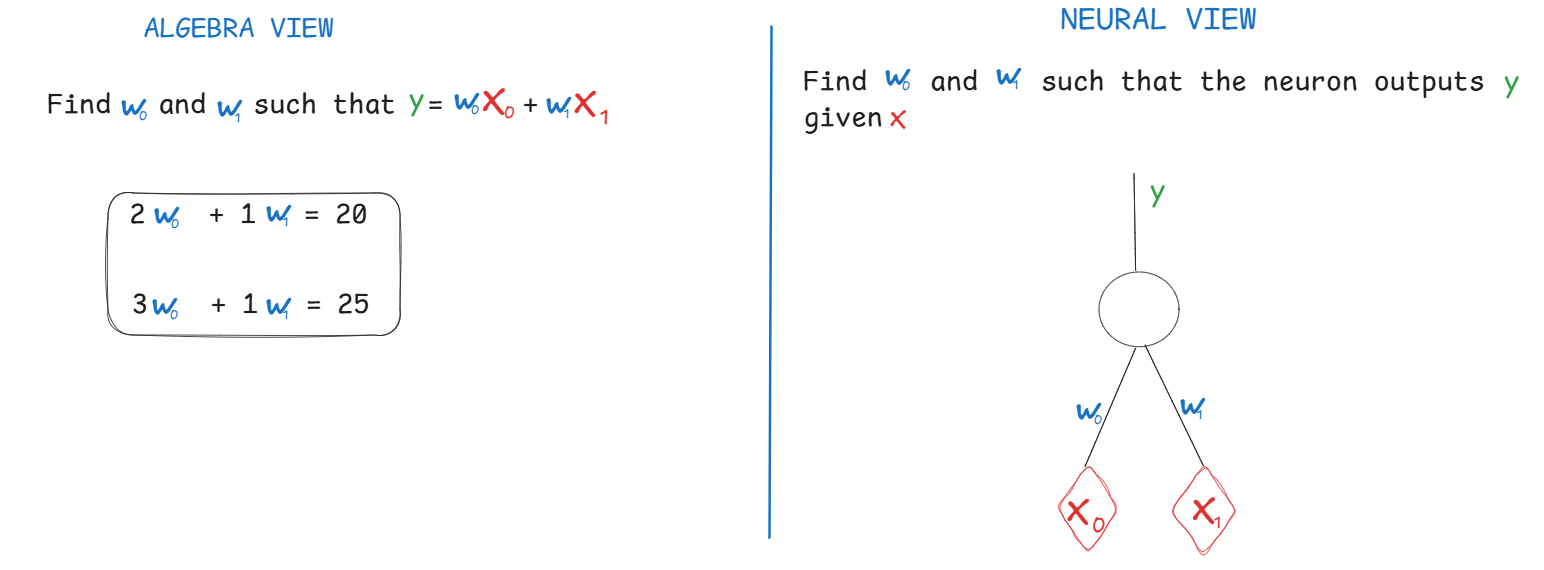
However, let us try a different approach:
- Randomly guess the weights (prices)
- Predict the total for each list
- Measure how bad our predictions are
- Update our weights using the "gradient"
- Repeat steps 2-4 until we are satisfied
The gradient is a number that tells us whether we should increase or decrease any given weight in order to reduce how bad our system is performing. This process is like the "hot or cold" game, where the gradient screams hot or cold at every iteration. You may wonder, "why would anyone solve the problem this way (gradient approach) instead of directly solving for the weights?"
Non-linear regression with feature extraction
Suppose that you are from Spain, where tomatoes are scarce, and the pricing follows the following model: Y = price_of_tomatoe × (number_of_tomatoes)² + price_of_cabbage × number_of_cabbage (eq 2.)
Remember you DON'T know the pricing model, and your task is to build a machine that can approximate it by solely looking at the input-output samples (the table above). If you attempt to approximate this system using (eq 1.), you will fail because of the non-linear term (tomatoes). You may be very smart or lucky and notice that your artificial model should use number_of_tomatoes² and not number_of_tomatoes. This is called feature extraction. Computer scientists have spent years perfecting feature extraction—the process of transforming complex, non-linear data in different domains into a form that linear models can handle effectively.
The input in our pricing problem only has 2 dimensions (tomatoes and cabbage). So feature extraction might not be too hard. But what if you have a system with 100 million dimensions? An iphone photo for example has about 30 million dimensions. If you want to predict how much time an instagram user would spend on a photo, or whether the user is looking at a dog or cat, good luck trying to find the non-linear term for each dimension. Clearly, it is an impractical approach to approximate every system using linear regression directly on the input, because you have to hunt down way too many non-linear terms if they exist. Let's now see why the gradient method is useful.
Deep layers
As shown in Figure 1, you can think of linear regression as a one neuron model. What if we used multiple neurons, such that the output of some neurons become the input to other neurons, and so forth.
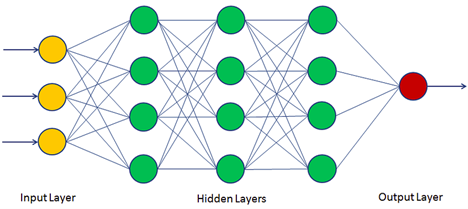
Each of the neurons in the hidden layers of Figure 2 has an additional function called "an activation function" or "non-linearity," which allows the system to handle non-linear inputs. Now, this artificial system, a deep neural network, can approximate any kind of system, both linear and nonlinear. In fact, neural networks are universal function approximators, as long as you have "enough" neurons and data to train them. Training uses the gradient approach: guess the weights at every neuron, predict output, measure how bad the prediction was, and update the weight using the gradient. "Oh wow, since this is so simple, why haven't we approximated every single useful system known to humans? Why haven't we approximated neurosurgeons yet?"
Challenges
The amount of data you need to train your model is a function of its size. The human brain has about 100 billion neurons. ChatGpt-3 has about 175 billion neurons, which are a lot simpler than real neurons, yet needed the entire internet to train[2].
Furthermore, data may be sufficient, but compute is not enough. It might take 100 years to train your AI car how to drive, but you want it to work within your lifetime, and your boss Elon Musk wants it within the next 6 months.
To that end, researchers try to find architectures and training techniques that require less data and compute time. For example, Yann LeCun found a good architecture to process images in the 1990s[3] and Google found one to train large language models like ChatGpt in 2017[4].
Conclusion
To facilitate understanding, some concepts were oversimplified, but the key concept is that most modern AIs are neural nets (function approximators) that are trained on huge amounts of data using gradient descent. As a result, we can copy systems like human drivers to build self-driving cars or our visual cortex to restore sight blind people [5]. To learn more, starting from scratch, follow Andrej Karpathy, one of the best AI researchers and instructors on the planet[6].